As Três Leis de Kepler
As Leis de Kepler afirmam que as órbitas são elípticas, que a velocidade aureolar
dos planetas é constante, e que a razão entre o cubo do período e o quadrado do
raio é constante. Leis de Kepler sobre o movimento planetário foram
desenvolvidas entre 1609 e 1619 pelo astrônomo e matemático alemão Johannes
Kepler.
As leis de Kepler são as três leis do movimento planetário definidas por Johannes Kepler, um matemático e astrônomo alemão. Essas leis foram a principal contribuição de Kepler à mecânica celeste.
"As leis do movimento planetário de Kepler são conhecidas como: lei das órbitas elípticas, lei das áreas e lei dos períodos. Juntas estas explicam como funciona o movimento de qualquer corpo orbitando algum astro massivo, como planetas ou estrelas. Vamos conferir o que se afirma nas leis de Kepler:"
1ª Lei de Kepler- “lei das órbitas”: A trajetória de cada planeta ao redor do Sol é uma elipse com o Sol em um dos focos.
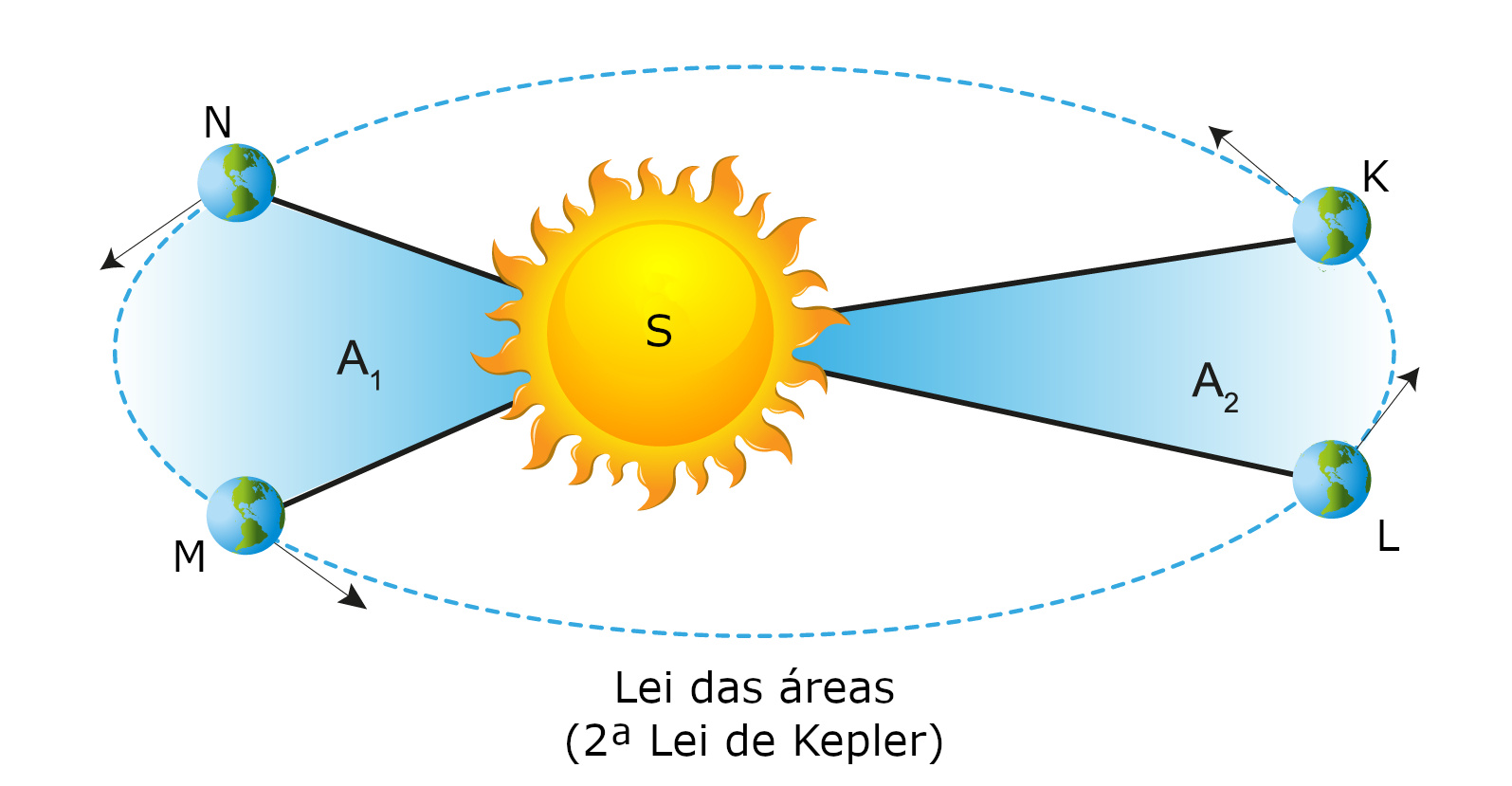
2ª Lei de Kepler- A reta que une um planeta ao Sol varre áreas iguais em intervalos de tempo iguais.
Equação da 2ª Lei de Kepler
Uma consequência deste fato é que a velocidade do planeta ao longo da sua trajetória orbital é diferente.
Sendo maior quando o planeta se encontra mais próximo do seu periélio (menor distância entre o planeta e o Sol) e menor quando o planeta se encontra próximo do seu afélio (maior distância do planeta ao Sol).
- quando o planeta vai do afélio para o periélio, seu movimento é acelerado;
- quando o planeta vai do periélio para o afélio, seu movimento é retardado;
3ª Lei de Kepler- “lei dos períodos”: O quadrado do período orbital de um planeta é diretamente proporcional ao cubo de sua distância média ao Sol.
Equação da 3ª Lei de Kepler
Em termos matemáticos, representando por T o período orbital de um certo planeta e por r sua distância média ao Sol (que equivale ao comprimento do semieixo maior da órbita), a terceira lei de Kepler pode ser expressa pela equação abaixo:
A forma mais conveniente da constante de Kepler é obtida por meio da aplicação da lei ao caso da Terra. Se a distância R for medida em unidades astronômicas (UA), que é uma unidade de medida de distância equivalente à distância média da Terra ao Sol, e o período orbital T for medido em anos, os respectivos valores correspondentes à Terra serão r = 1 UA e T = 1 ano. Aplicada a terceira lei de Kepler, a constante K assume o valor 1 e a relação fica resumida à expressão:
Exemplo aplicado:
1) (UFRGS - 2011) Considere o raio médio da órbita de Júpiter em tomo do Sol igual a 5 vezes o raio médio da órbita da Terra. Segundo a 3ª Lei de Kepler, o período de revolução de Júpiter em tomo do Sol é de aproximadamente:
a) 5 anos
b) 11 anos
c) 25 anos
d) 110 anos
e) 125 anos
2) Certo planeta A, que orbita em torno do Sol, tem período orbital de 1 ano. Se um planeta B, tem raio orbital 3 vezes maior, qual será o tempo necessário para que esse planeta complete uma volta em torno do Sol.
a) 1,5 anos
b) 2,5 anos
c) 8,0 anos
d) 3,5 anos
e) 5,2 anos
3) O raio médio do planeta Marte é cerca de quatro vezes maior que o raio médio da órbita do planeta Mercúrio. Se o período de revolução Mercúrio é 0,25 anos, qual é o período de revolução Marte?
Leis de Kepler e a Gravitação Universal
As Leis de Kepler descrevem o movimento dos planetas, sem se preocupar com as suas causas. Isaac Newton ao estudar essas Leis, identificou que a velocidade dos planetas ao longo da trajetória é variável em valor e direção.
Para explicar essa variação, ele identificou que existiam forças atuando nos planetas e no Sol.
Deduziu que essas forças de atração dependem da massa dos corpos envolvidos e das suas distâncias.
Chamada de Lei de Gravitação Universal, sua expressão matemática é:
Sendo:
F: força gravitacional
G: constante de gravitação universal= G = 6,7 · 10 Nm/kg
M: massa do Sol
m: massa do planeta
d² é o quadrado da distância que os separa.
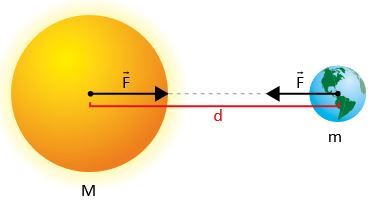
Sejam duas massas m1 e m2, em que d é a distância entre seus centros.
- A força gravitacional é sempre de atração
- A força gravitacional não depende do meio onde os corpos se encontram imersos.
- A constante da gravitação universal G teve seu valor comprovado experimentalmente por Henry Cavendish por meio de um instrumento denominado balança de torção. G = 6,7 · 10 Nm/kg
Exemplo resolvido:
4) Considere que os centros de massa de duas pessoas adultas estão separados pela distância de 2,0 m e que suas massas são aproximadamente iguais a 100 kg. A intensidade da força de atração gravitacional entre elas é um valor mais próximo de? Dado: constante da gravitação universal
G = 6,7 · 10 Nm/kg
a) 1,7 x 10–7N.
b) 3,4 x 10–7N.
c) 1,7 x 10–1N.
d) 3,4 x 10–1 N.
e) 1,7 x 10–6N.
Nenhum comentário:
Postar um comentário